State-Space Frequency-Domain Adaptive Filter: State-Space FDAF
"State-Space FDAF" is an adaptive filter algorithm that has its roots in Kalman filter theory and thus uses "state-space" terminology. At the same time, State-Space FDAF can be seen as a direct evolution of the widely used frequency-domain adaptive filter, a.k.a. known as block LMS, and thus the "FDAF" terminology. Furthermore, "State-Space FDAF" and "Frequency-domain adaptive Kalman filter", as introduced in [1], are by and large equivalent and synonymous. The term "State-Space FDAF" better conveys its ingredients and the fact that the exact Kalman filter is approximated here.
State-Space FDAF was found in the field of acoustic signal processing to achieve both fast and robust adaptation of long acoustic echo control filters [1]. In this application, the key to arrive at State-Space FDAF is an acoustic state-space model of the acoustic environment. The figure below describes the underlying model together with two possible use cases of State-Space FDAF. At the left, an acoustic environment is represented by the point-to-point transfer function W(z), which evolves according to a first order Markov model. In that model, the system function W(z) is updated after a delay T and a forgetting factor A by an incremental stochastic quantity dW(z). The system function W(z) is termed the unknown acoustic state. It is observed as Y(z) in the presence of additive observation noise S(z), which may represent ambient noise or local speech.
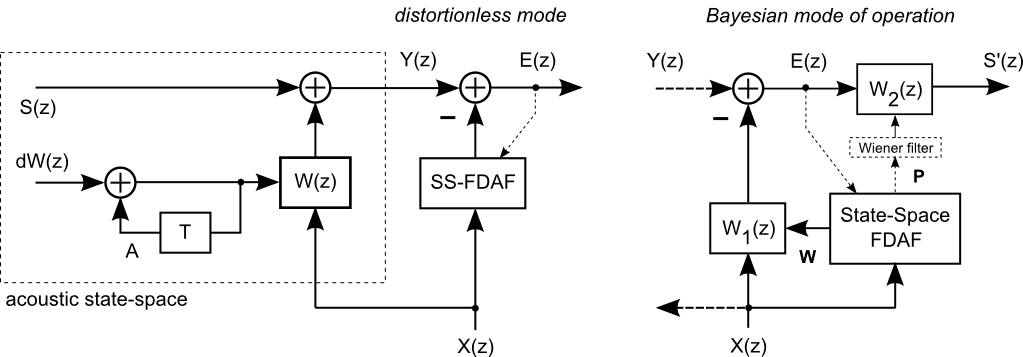
In a "distortionless mode", see left part of the picture, the State-Space FDAF algorithm operates as an adaptive filter with reference input X(z) to minimize the adaptive filter output error E(z). The State-Space FDAF algorithm in this mode adapts to the time-varying acoustic state W(z) in order to cancel as much X(z) related signal as possible from the observation Y(z), while the independent signal S(z) remains untouched in this mode. In the "Bayesian mode of operation", at the right, the State-Space FDAF algorithm explicitly performs acoustic system identification in that it finds the posterior mean W and covariance P of the acoustic state W(z), subject to the underlying acoustic state-space model. The posterior mean W is then used to control a distortionless cancellation of X(z) related signal, while the state-error covariance P is translated to an open-loop Wiener postfilter that performs statistical suppression of unavoidable residual signal related to X(z). The latter comes with a minimum of unavoidable distortion of S(z). The final output S'(z) then represents a minimum mean-square error estimate of S(z). [1]
In both cases, State-Space FDAF unites the known features of frequency-domain adaptive filtering, such as
- its attractively low computational complexity via FFT/IFFT-based convolution and correlation, and
- its fast convergence despite auto-correlation of the reference input X(z), e.g., in speech applications,
with the well appreciated characteristics of the Kalman filtering technique, i.e.,
- an optimal balance of fast and robust tracking of time-varying systems W(z),
- an elegant unification of adaptive filtering and adaptation control, e.g., an inherent stepsize control function, and
- the delivery of the reliability information P along with the state estimate W.
Generalizations of the State-Space FDAF algorithm have been presented for cases with single-input multiple-output (SIMO) system functions [2], and for applications with Hammerstein nonlinear acoustic state-space models [3,4].
[1] G. Enzner and P. Vary, "Frequency-Domain Adaptive Kalman Filter for Acoustic Echo Control in Hands-free Telephones", Signal Proc., Elsevier, vol. 86, no. 6, pp. 1140-1156, June 2006
[2] S. Malik and G. Enzner, "Recursive Bayesian Control of Multichannel Acoustic Echo Cancellation", IEEE Signal Proc. Lett., vol. 18, no. 11, pp. 619-622, Nov. 2011
[3] S. Malik and G. Enzner, "State-Space Frequency-Domain Adaptive Filtering for Nonlinear Acoustic Echo Cancellation", IEEE Trans. Audio Speech and Language Proc., vol. 20, no. 7, pp. 2065-2079, Sept. 2012
[4] S. Malik and G. Enzner, "A Variational Bayesian Learning Approach for Nonlinear Acoustic Echo Control", IEEE Trans. Signal Proc., vol. 61, no. 23, pp. 5853-5867, Dec. 2013
