Normalized Filter-Projection Misalignment: NFPM
The NFPM is a system-distance measure for single-input multiple-output (SIMO) systems. Given two different SIMO systems, the NFPM projects the first system on the second system via a single-input single-output (SISO) system. That SISO system is applied commonly to each branch of the first SIMO system, such that its projection matches the second SIMO system in the least-squares sense. The respective least-squares error is termed NFPM [1].
In this way, the NFPM disregards a common-filter deviation between two SIMO system, i.e., NFPM indicates a small misalignment between two SIMO systems whenever the misalignment of two SIMO systems merely consists in a common filter between the individual branches of the SIMO systems. The NFPM thus evaluates how closely the diverse parts the two SIMO systems match with each other. The diverse part of a SIMO system, i.e., its coprime part, in turn is of particular value in applications of multichannel signal processing and communication.
An example of two SIMO systems is depicted below. The left system comprises individual transfer functions Hc(z) Hi(z), where Hc(z) describes a common part and Hi(z) the diverse part of that system. At the right the common part is Hp(z) and the diverse part H'i(z). In the calculation process of the NFPM, the SISO-based projection will effectively unfilter the common part Hc(z) from the left system and introduce Hp(z) in the same place. This only requires knowledge of the available transfer functions Hc(z) Hi(z) and Hp(z) H'i(z), i.e., not of the typically unavailable common parts Hc(z) and Hp(z). As a result, NFPM effectively evaluates the square-error distance of the diverse parts Hi(z) and H'i(z).
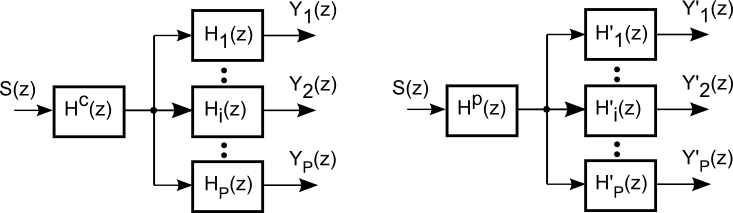
This example application of NFPM is of relevance in the field of multichannel blind SIMO system identification. Here the system identification is performed on the basis of the system outputs Yi(z) alone. It was shown for instance in [2] that the blind identification of the left system will drop the undetectable common-zeros part Hc(z) and rather deliver a random common phantom-zeros part Hp(z) in place of Hc(z). NFPM thus evaluates the performance of multichannel blind SIMO identification with a particular focus on the diverse part of the system, i.e., disregarding unavoidable common filtering errors.
NFPM is a generalization of the widely used NPM (normalized projection misalignment), which was deployed for the evaluation of blindly estimated impulse response in applications with uncertain reference to the input signal level. NPM merely uses a gain factor in place of NFPM's SISO-based projection and is thus limited to the evaluation of multichannel blind SIMO identification in the absence of common zeros Hc(z) in the unknown system. NFPM relaxes those strict identifiability conditions and proves the value of multichannel blind SIMO identification despite the presence of common zeros [2].
[1] D. Schmid and G. Enzner, "Evaluation of adaptive blind SIMO identification in terms of a normalized filter-projection misalignment", IEEE Intl. Conf. Acoustics Speech and Signal Proc., Prague, May 2011
[2] D. Schmid and G. Enzner, "Cross-Relation-Based Blind SIMO Identifiability in the Presence of Near-Common Zeros and Noise", IEEE Trans. on Signal Processing, vol. 60, no. 1, pp. 60-72, Jan. 2012
