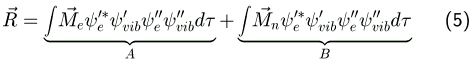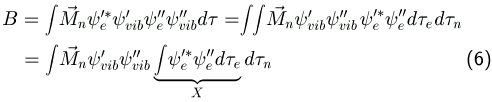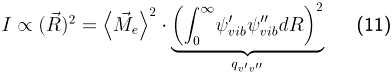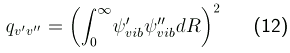Herleitung der Franck-Condon-Faktoren
Im wesentlichen entspricht diese Herleitung Herzberg, Kap. IV, 4.
Die Intensität I eines elektrischen Dipol-Übergangs ist laut Atkins, Kapitel 8,
proportional zu dem Quadrat des Übergangsdipolmoments:
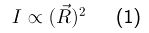
(Frage: welche anderen Arten von Übergängen gibt es?)
Das Übergangsdipolmoment kann geschrieben werden als
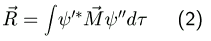
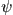 ' und
' und
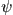 '' sind die Wellenfunktionen des oberen
bzw. des unteren beteiligten Zustands. Der Index * steht für konjugiert-komplex.
'' sind die Wellenfunktionen des oberen
bzw. des unteren beteiligten Zustands. Der Index * steht für konjugiert-komplex.
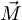 ist der
Dipolmomentoperator. Es wird über alle Koordinaten
ist der
Dipolmomentoperator. Es wird über alle Koordinaten 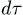 integriert.
integriert.
Unter Annahme der Born-Oppenheimer-Näherung (Elektronenbewegung ist viel schneller als die Bewegung der Kerne) kann
die Wellenfunktion als Produkt einer elektronischen Wellenfunktion und einer Kernwellenfunktion geschrieben
werden. Zur Vereinfachung wird die Gerüstrotation vernachlässigt, so daß der Kernanteil nur noch die Vibration beschreibt.
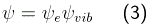
Der Dipolmomentoperator läßt sich in einen elektronischen Anteil (abhängig von den Elektronenkoordinaten) und einen Kernanteil
(abhängig von den Kernkoordinaten) aufteilen.
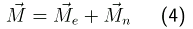
(Frage: wie ist das Dipolmoment definiert?)
Gleichung 2 läßt sich dann als Summe zweier Integrale ausdrücken:
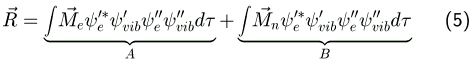
Die Vibrationswellenfunktionen sind reell, daher kann das *-Symbol für konjugiert-komplex weggelassen werden.
Weil 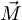 n und die Vibrationswellenfunktionen
n und die Vibrationswellenfunktionen
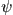 vib nicht von den Elektronenkoordinaten
abhängen, kann Teil B umgeformt werden zu:
vib nicht von den Elektronenkoordinaten
abhängen, kann Teil B umgeformt werden zu:
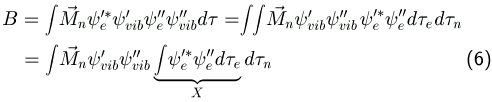
Die elektronischen Wellenfunktionen 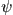 e
werden weiterhin sowohl über die Kernkoordinaten
e
werden weiterhin sowohl über die Kernkoordinaten
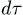 n als auch über die Elektronenkoordinaten
n als auch über die Elektronenkoordinaten
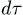 e integriert.
e integriert.
Eine Eigenschaft der Lösungen der Schrödingergleichung ist die Orthogonalität: integriert man das Produkt zweier Wellenfunktionen, die
unterschiedliche Zustände desselben Systems beschreiben, über alle Koordinaten, so erhält man Null. Das gilt auch für
unterschiedliche elektronische Zustände eines Moleküls. Daher ist der Teil X aus Gleichung 6 gleich Null:
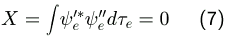
Und somit ist der gesamte Teil B gleich Null. Es bleibt bei der Berechnung von
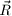 noch Teil A:
noch Teil A:
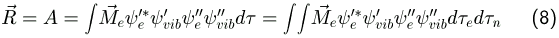
Auch hier sind die Vibrationswellenfunktionen unabhängig von den Elektronenkoordinaten, daher:

<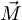 e>
ist der Erwartungswert des elektronischen Dipolübergangsmoments. Oft ist
<
e>
ist der Erwartungswert des elektronischen Dipolübergangsmoments. Oft ist
<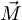 e>
wenig oder gar nicht von den Kernkoordinaten abhängig, daher kann Gleichung 9 umgeformt werden zu:
e>
wenig oder gar nicht von den Kernkoordinaten abhängig, daher kann Gleichung 9 umgeformt werden zu:
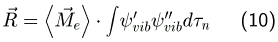
Laut Gleichung 1 ist die Intensität proportional zu dem Quadrat von 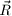 .
Für zweiatomige Moleküle kann man
.
Für zweiatomige Moleküle kann man 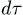 n durch
dR (mit R = Abstand der beiden Atome) ersetzen und erhält für die Intensität:
n durch
dR (mit R = Abstand der beiden Atome) ersetzen und erhält für die Intensität:
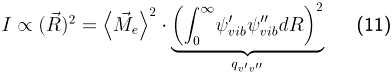
Geht man davon aus, daß
<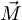 e>
konstant ist, dann sind die relativen Intensitäten nur proportional zu den Franck-Condon-Faktoren
e>
konstant ist, dann sind die relativen Intensitäten nur proportional zu den Franck-Condon-Faktoren
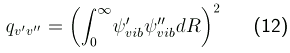
zurück