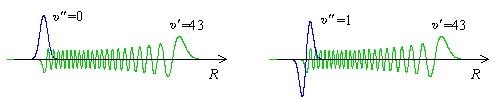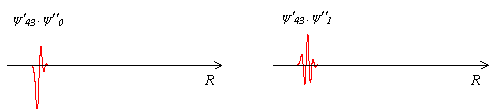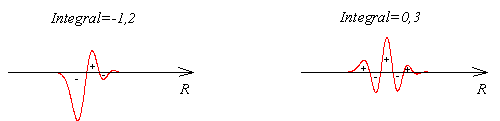Berechnung von Franck-Condon-Faktoren
Hier soll die Berechnung der Franck-Condon-Faktoren q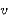 '=43,
'=43,
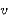 ''=0 und
q
''=0 und
q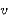 '=43,
'=43,
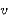 ''=1
durchgeführt werden. Dazu wird der Ausdruck
''=1
durchgeführt werden. Dazu wird der Ausdruck
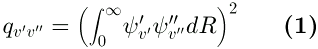
von innen nach außen "abgearbeitet".
Die an den Übergängen (B, 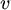 '=43
'=43
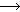 X,
X,
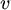 ''=0) und
(B,
''=0) und
(B, 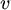 '=43
'=43
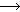 X,
X,
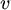 ''=1) beteiligten Potentialkurven und
Vibrationswellenfunktionen sind in Abbildung 1 dargestellt (Potentialkurven: schwarz, Vibrationsenergieniveaus:
rot, Vibrationswellenfunktionen im el. Zustand X: blau, Vibrationswellenfunktionen im el. Zustand B: grün):
''=1) beteiligten Potentialkurven und
Vibrationswellenfunktionen sind in Abbildung 1 dargestellt (Potentialkurven: schwarz, Vibrationsenergieniveaus:
rot, Vibrationswellenfunktionen im el. Zustand X: blau, Vibrationswellenfunktionen im el. Zustand B: grün):
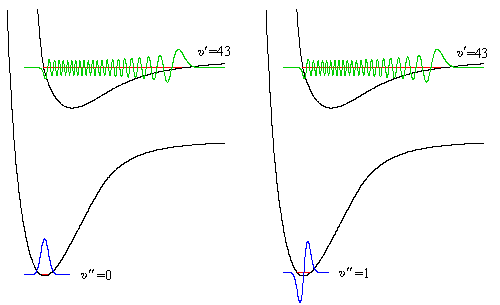
Abbildung 1
Die Born-Oppenheimer-Näherung besagt, daß die Atomkerne sich im Vergleich zu den Elektronen
so langsam bewegen, daß sie als stationär anzusehen sind. Vor und nach dem elektronischen Übergang haben die Kerne
also fast dieselbe Position und Geschwindigkeit.
Weil sich die Position während des elektronischen Übergangs nicht ändert, stimmt die R-Achse für
beide Schwingungswellenfunktionen 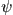 ' und
' und
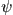 '' überein.
Daher können die beiden Wellenfunktionen gemeinsam auf einer Achse dargestellt werden:
'' überein.
Daher können die beiden Wellenfunktionen gemeinsam auf einer Achse dargestellt werden:
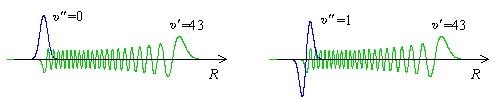
Abbildung 2
Wegen der Voraussetzung, daß sich die Positionen der Kerne während des Übergangs nicht ändern, wird in
vielen Lehrbüchern von einem "vertikalen Übergang" gesprochen.
Der erste Schritt zur Berechnung der Franck-Condon-Faktoren ist die Bildung des Produktes
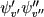 der beiden Vibrationswellenfunktionen. Man erhält es,
indem man für jeden Wert R die Funktionswerte
der beiden Vibrationswellenfunktionen. Man erhält es,
indem man für jeden Wert R die Funktionswerte 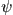 '(R)
und
'(R)
und 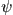 ''(R) miteinander multipliziert. In Abbildung 3 ist
die resultierende Funktion rot dargestellt.
''(R) miteinander multipliziert. In Abbildung 3 ist
die resultierende Funktion rot dargestellt.
Auffällig ist, daß nur ein enger Bereich bei kleinem R von Null verschieden ist. Der Grund dafür ist, daß für beide Fälle
die Wellenfunktion 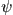 '' bei höheren R gleich Null
ist.
'' bei höheren R gleich Null
ist.
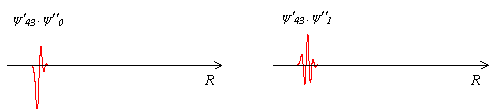
Abbildung 3
Der zweite Schritt ist die Integration der Produktfunktionen. In Abbildung 4 sind diese vergrößert dargestellt.
Das Integral 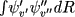 einer Funktion ist die Fläche
unter dem Graphen. Man beachte, daß die Fläche unterhalb der R-Achse ein negatives Vorzeichen hat.
Es wird über den gesamten Definitionsbereich integriert, also von R = 0 bis unendlich.
einer Funktion ist die Fläche
unter dem Graphen. Man beachte, daß die Fläche unterhalb der R-Achse ein negatives Vorzeichen hat.
Es wird über den gesamten Definitionsbereich integriert, also von R = 0 bis unendlich.
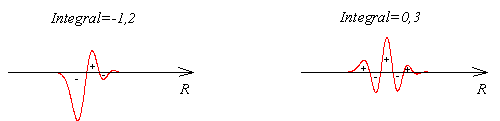
Abbildung 4
Bei der linken Funktion überwiegen die negativen Flächen, daher ist ihr Integral negativ. Bei der rechten Funktion heben sich
positive und negative Flächen fast auf. Das Integral ist positiv, hat aber einen kleineren Betrag als das Integral der linken Funktion.
Der letzte Schritt besteht darin, die erhaltenen Werte zu quadrieren. Für die linke Funktion erhält man 1,44 und für die rechte 0,09.
Das Verhältnis
q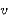 '=43,
'=43,
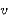 ''=0 / q
''=0 / q
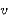 '=43,
'=43,
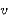 ''=1 der Franck-Condon-Faktoren beträgt also
1,44 / 0,09 = 16.
''=1 der Franck-Condon-Faktoren beträgt also
1,44 / 0,09 = 16.
(Anmerkung: die absoluten Werte der Franck-Condon-Faktoren sind hier nicht korrekt wiedergegeben: die Summe aller Franck-Condon-Faktoren
eines elektronischen Übergangs ist eins.)
zurück