|
O P A R - Open Architecture Particle in Cell Simulation - Version 3.0
Plasma simulations with dust particles
|
|
O P A R - Open Architecture Particle in Cell Simulation - Version 3.0
Plasma simulations with dust particles
|
Solves Poisson equation using a multigrid method for 2D and 3D simulations. The Poisson equation is given by 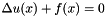 where
where 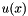 is the unknown scalar field (plasma potential). The outer boundary condition is set to zero, this means on the very outer grid points of the simulation box
is the unknown scalar field (plasma potential). The outer boundary condition is set to zero, this means on the very outer grid points of the simulation box 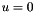 is set. The grid points on the surface of the dust particle(s) is set as a inner boundary condition according to the surface potential of the dust particle(s), calculated from the dust charge, see Potential. This inner boundary condition is time-dependent and can be different in the next timestep, because the charge of the dust particle(s) can change. To follow the spherical surface, reduced grid spacings are used here, which are calculated und stored in the beginning of a simulation, see ClosedGeometry. Periodic boundary conditions are not implemented. For 1D simulations a tridiagonal matrix solver is implemented.
More...
is set. The grid points on the surface of the dust particle(s) is set as a inner boundary condition according to the surface potential of the dust particle(s), calculated from the dust charge, see Potential. This inner boundary condition is time-dependent and can be different in the next timestep, because the charge of the dust particle(s) can change. To follow the spherical surface, reduced grid spacings are used here, which are calculated und stored in the beginning of a simulation, see ClosedGeometry. Periodic boundary conditions are not implemented. For 1D simulations a tridiagonal matrix solver is implemented.
More...
#include <poisson.h>
Public Member Functions | |
| Poisson (Geometry *geom_) | |
| The default constructor reads the attributes from global variables. | |
| void | solve (grid< double > &u, grid< double > &f, double potd[20]) |
Solves the poisson equation 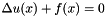 . . | |
Protected Attributes | |
| double | dx |
| Grid spacing in x direction. | |
| double | dy |
| Grid spacing in y direction. | |
| double | dz |
| Grid spacing in z direction. | |
| int | nu1 |
| Do nu1 Gauss steps then repeat multigrid refinement gama times then do nu2 Gauss steps. | |
| int | nu2 |
| int | Rg |
| Dust particle radius. | |
| int | nd |
| Number of dust particles in the simulation. | |
| int | ig |
| Number of gird points at the dust particle(s) | |
| double | epsilon |
| The error to reach. | |
| std::valarray< double > | potd |
| Surface potential of the dust particle(s) | |
| Geometry * | geom |
| Pointer to the reference geometry. | |
| Wall * | pWall |
| Pointer to the reference wall. | |
| Potential * | pPotential |
| Pointer to the reference potential. | |
Solves Poisson equation using a multigrid method for 2D and 3D simulations. The Poisson equation is given by 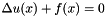 where
where 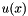 is the unknown scalar field (plasma potential). The outer boundary condition is set to zero, this means on the very outer grid points of the simulation box
is the unknown scalar field (plasma potential). The outer boundary condition is set to zero, this means on the very outer grid points of the simulation box 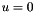 is set. The grid points on the surface of the dust particle(s) is set as a inner boundary condition according to the surface potential of the dust particle(s), calculated from the dust charge, see Potential. This inner boundary condition is time-dependent and can be different in the next timestep, because the charge of the dust particle(s) can change. To follow the spherical surface, reduced grid spacings are used here, which are calculated und stored in the beginning of a simulation, see ClosedGeometry. Periodic boundary conditions are not implemented. For 1D simulations a tridiagonal matrix solver is implemented.
is set. The grid points on the surface of the dust particle(s) is set as a inner boundary condition according to the surface potential of the dust particle(s), calculated from the dust charge, see Potential. This inner boundary condition is time-dependent and can be different in the next timestep, because the charge of the dust particle(s) can change. To follow the spherical surface, reduced grid spacings are used here, which are calculated und stored in the beginning of a simulation, see ClosedGeometry. Periodic boundary conditions are not implemented. For 1D simulations a tridiagonal matrix solver is implemented.
 1.8.1.1
1.8.1.1